P5663 [CSP-J2019] 加工零件 题解
这题有点思维含量,但是还行。 然而考试时脑抽没想到.png
题意比较清楚,所以我们直接看做法
解题思路
部分分思路
很容易想到 dfs 电风扇 暴力求解 ,于是光荣地 T 飞了。代码就不放了,大家都会写。
当然,也有一些优化措施。
一般,考场上写暴力的话能写出 40pts 的代码,只有前 8 个点。
经过一些记忆化处理,可以骗到 60pts。
再经过一些对 memset 毒瘤处理,可以再骗走 20pts。
具体方法可以看这篇题解。
AC 思路
考虑最短路
根据题意我们可以设原材料为 $0$ 阶段的零件
先看这张图:
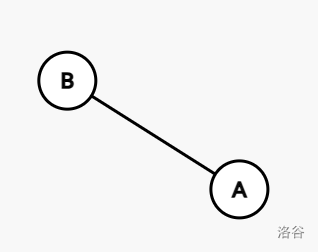
我们可以发现如果 $A$ 想生产 $L$ 阶段 $(L≥2)$ 的零件,就需要 $B$ 生产 $L-1$ 阶段的零件,就需要 $A$ 生产 $L-2$ 阶段的零件。
所以问题的实质就是看 $A$ 和 $B$ 之间有没有长度为 $L$ 的路径。
仔细思考,我们可以发现:如果 $A$ 到 $B$ 有长度为 $X$ 的路径,则 $A$ 到 $B$ 一定有长度为 $(X + n * 2)$ 的路径,但不一定有长度为 $(X + n * 2 - 1)$ 的路径。$(n \ge 1)$
所以,我们要对每个点求一遍奇数路径,和偶数路径。
AC Code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
| #include <bits/stdc++.h>
#define int long long
using namespace std;
const int N = 1e5 + 5;
int n, m, q, ji[N], ou[N];
bool vis[N];
vector<int> e[N];
void bfs()
{
memset(ji, 0x3f, sizeof(ji));
memset(ou, 0x3f, sizeof(ou));
memset(vis, 0, sizeof(vis));
queue<int> q;
ou[1] = 0;
vis[1] = 1;
q.push(1);
while (!q.empty())
{
int u = q.front();
q.pop();
vis[u] = 0;
for (auto v : e[u])
{
if (ou[u] + 1 < ji[v])
{
ji[v] = ou[u] + 1;
if (!vis[v])
q.push(v), vis[v] = 1;
}
if (ji[u] + 1 < ou[v])
{
ou[v] = ji[u] + 1;
if (!vis[v])
q.push(v), vis[v] = 1;
}
}
}
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0), cout.tie(0);
cin >> n >> m >> q;
for (int i = 1; i <= m; i++)
{
int u, v;
cin >> u >> v;
e[u].push_back(v);
e[v].push_back(u);
}
bfs();
while (q--)
{
int a, l;
cin >> a >> l;
if (l % 2 == 0)
{
if (ou[a] > l)
puts("No");
else
puts("Yes");
}
else
{
if (ji[a] > l)
puts("No");
else
puts("Yes");
}
}
}
|
